Field
Rotation, Polar Alignment, and
Declination Drift
Calculations, Formulas and
Relation
to Astrophotography
Part
I: Altitude-azimuth mounts
When using an alt-azimuth mount to look at things in the sky, even with
a mount that is capable of tracking the stars (such as the Meade LX200
series), images will appear to rotate within the eyepiece field. This
phenomenon
is known as field rotation.
It is easy to understand how this arises by considering a specific
example. Imagine we are at the equator looking at a pair of stars very
near the north (or south) pole - i.e. very close to the horizon - such
that the two stars happen to have the same Right Ascension (RA). Let's
draw a line through
them; in fact this line will coincide with their RA line. As the stars
rise
above the horizon, this line will be almost parallel to the horizon.
When
the stars pass through the meridian, this line will be vertical with
the
horizon; in fact it will coincide with the meridian. Finally as the
stars
set the line will once again be parallel to the horizon again. Now
imagine
that we are looking at the stars with a telescope and - for our current
purposes - an eyepiece with a rectangular field of view such that one
side
of the rectangle is parallel to the horizon. The manner by which
alt-azimuth
mounts work ensure that this side of the rectangle would always remain
parallel
to the horizon (remember lines of constant altitude are parallel to the
horizon). However, I just mentioned that the line drawn through our
pair
of stars will appear to rotate with respect to the horizon, which means
when viewed through our rectangular telescope field of view they will
certainly
rotate as well. With a little extra thought, it is easy to see that
this
field rotation is really independent of the shape of the eyepiece field
of view.
Field rotation isn't really an issue for visual observing, but when
trying to perform astrophotography, field rotation means that there is
a certain maximum exposure time you can use for an alt-azimuth mount
driven photographic instrument before your stars become recorded as
arcs.
This page describes my attempts to calculate the exact magnitude of
field rotation as a function of the astronomer's latitude. Following
which I will also try to derive an expression for the maximum exposure
time allowed before noticeable image smearing occurs, specifically in
the context of high power planetary photography. I shall assume the
reader understands multivariable and vector calculus, as well as some
very elementary ideas from differential geometry. Please do let me know
if you spot any computational or other mathematical errors.
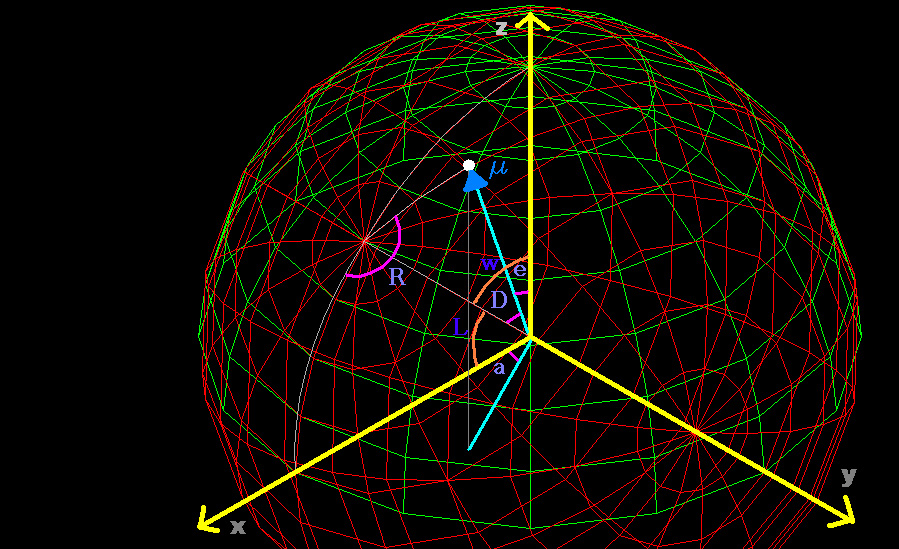
For convenience let's imagine our stars are all stuck on a unit sphere
and we as observers are mathematical points right at the center of the
sphere. For a given object in the sky (i.e. on the unit sphere), we can
specify
its coordinates by using a cartesian system (x, y, z). This can
also
be related to its right ascension and declination, or to its altitude
and
azimuth. Let's spend some time setting up these two different sets of
coordinates
on the unit sphere. (You may wonder why we need two sets of coordinates
-
please read on to find out.)
Let's start with the altitude-azimuth coordinates. If we let the x-y
plane represent the apparent plane (horizon) we observe from, the z
axis would
point to the zenith. Given a star on the sphere, let the angle
subtended
by the z axis and the radial line joining the star and our sphere
center
(also the center of our x-y-z axes) be e. Project the star
perpendicularly
upon the x-y plane and draw a line from the projected point to (0,0,0).
Denote
the angle subtended by this line and the x axis as a. These {e, a}
coordinates are very similar to altitude and azimuth coordinates,
except that I've chosen them this way to help make calculations easier.
We thus have, the coordinates of a given point on the sphere µ[e,
a] = (x, y, z) = (sin[e] cos[a], sin[e] sin[a], cos[e]).
Let's set up the right ascension-declination-like coordinates. Because
we won't really be interested in the exact right ascension of the
objects
in question, I propose to use the following system to make calculations
easier. Imagine that in place of the above {e, a} coordinates, I change
their names to {R, D} instead. Then I rotate the whole sphere about the
y axis by an angle w (without rotating the axes themselves - otherwise
we're
back to the same situation). Notice this set of new rotated {R, D}
coordinates
is similar to an RA-Dec system for a latitude of (90 degrees - w
degrees).
Mathematically this means we replace the above {e, a} with {R, D}
and multiply the above vector by a rotation matrix.
After some trigonometry and linear algebra we have µ[R, D] = (x, y, z) =
(cos[R]
cos[w] sin[D] + cos[D] sin[w], sin[D] sin[R], cos[D] cos[w] - cos[R]
sin[D]
sin[w]).
But I'd ultimately want my formulas in terms of R, D so it'd be more
convenient to shift coordinates such that the sines and cosines of w
appears with the e and a. But since rotation matrices are easy to
invert we obtain immediately
µ[R, D] = (x, y,
z) = (sin[R] cos[D], sin[R] sin[D], cos[R]) = µ[e, a] = (x, y, z) =
(cos[e]
cos[w] sin[a] - cos[a] sin[w], sin[a] sin[e], cos[a] cos[w] + cos[e]
sin[a]
sin[w]).
An alt-azimuth mount that tracks the stars is one that moves in such a
way that a scope mounted on it will point always at the same
constant-declination line in
the sky (i.e. on the unit sphere). Imagine that we can see two sets of
finely
spaced grids superimposed on our sky as we look through a telescope
mounted
on such a mount: one set is that of the altitude-azimuth, and the other
the RA-Dec. Because ours is a alt-azimuth mount, the altitude-azimuth
grid
will not appear to rotate as we follow the stars, but the RA-Dec lines
would,
for the reasons already discussed earlier; whereas the orientation of
objects in the sky (e.g. the direction of the line drawn through our
hypothetical pair of stars) stay fixed with respect to the RA-Dec grid
(e.g. the line through the 2 stars stay on top of a particular
constant-RA line). This makes us realize that field
rotation at a given point in the sky is really the rate of change of
the
angle formed by either the RA line or the Dec line with the azimuth or
altitude
line passing through it as we move along in RA while tracking the
stars.
In more technical language, we need to obtain two frames at every
point on the sphere: one with unit vectors parallel to the RA and Dec
lines
passing through the given point, and the other with unit vectors
parallel
to the azimuth and altitude lines passing through the same. As the
mount
tracks, it moves in RA; but because it is an alt-azimuth mount, it
"remains"
set in the latter frame field, while the former RA-Dec frame field
rotates
with respect to the latter.
Since we are interested in angles only, we need only to obtain one
vector for each frame.
For the RA-Dec frame, I got the vector pointing parallel to the
constant Dec line by differentiating µ[R, D] with respect to R,
to
obtain dµ/dR =
(-Sin[D]
Sin[R], Cos[R] Sin[D], 0). By taking dot product with itself, we see
the
length of the vector is (Sin[D])^2, and so the unit vector is r_hat =
(1/Sin[D)
(-Sin[D] Sin[R],
Cos[R]
Sin[D], 0).
For the altitude-azimuth frame, I got the vector pointing parallel to
the constant altitude line by differentiating µ[R, D] with respect to e,
to
obtain dµ/de = (Cos[D] Cos[R] dD/de
-
dR/de Sin[D] Sin[R], Cos[R] dR/de Sin[D] + Cos[D] dD/de Sin[R], dD/de
Sin[D]).
Taking dot products with itself we see its length is (dD/de^2 + dR/de^2
Sin^2[D])^0.5. The corresponding unit vector is thus E_hat = (dD/de^2 + dR/de^2
Sin^2[D])^0.5
(Cos[D] Cos[R] dD/de - dR/de
Sin[D] Sin[R], Cos[R] dR/de Sin[D] + Cos[D] dD/de Sin[R], dD/de Sin[D]).
We need to figure out what dD/de and dR/de are. To do that we refer to
the fact that µ[R,
D] = µ[e, a]
since
they really are the same vector. Look at the z component of the matrix
equation:
cos[e] = cos[D]
cos[w]
- cos[R] sin[D] sin[w]. By differentiating both sides with respect to
R,
with respect to D, using the relation sin^2 + cos^2 = 1, and using the
fact
that dx/dy = 1/(dy/dx), we can then obtain dR/de and dD/de.
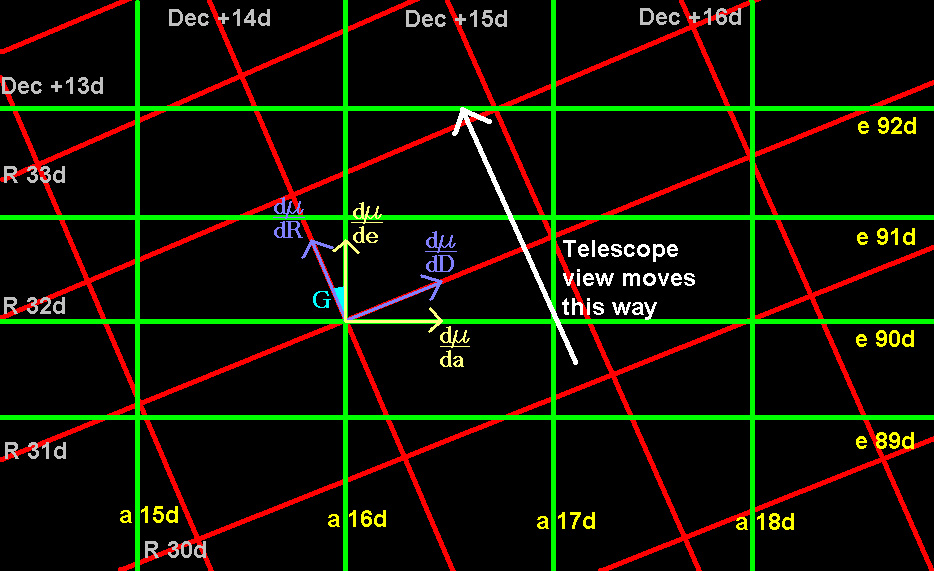
A "zoomed-in" view of the two
sets of coordinate systems around a given point on the celestial
sphere. The two frames used in our calculations are shown with the
un-normalized vectors. It is difficult to draw curved lines, so I drew
straight lines - in reality, coordinate lines are curved. With some
imagination, one can see how
field rotation occurs: the alt-azimuth mounted telescope delivers a
view in which the {e, a} frame (indicated by the dµ/de and dµ/da vectors) does not
rotate; and at the same tine the orientation of the celestial objects
stay fixed with respect to the RA-Dec grid (and hence with respect to
the
{R, D} frame, indicated by the dµ/dR and dµ/dD vectors). Now the telescope, if tracking,
moves along in RA (or, in our system of variables, simply R). Because
the coordinate lines are generally curved, the angle G between the
frame vectors dµ/dR
and dµ/de will
change as R changes, giving rise to field rotation. This way of
thinking about field rotation also forms the basis of our calculations.
(Note that I have made no effort to make the R, Dec, e, and a scales
consistent, because they are merely there for illustrative purposes.
For instance, {e, a} = {90d, 16d} is most certainly not the same point
as {R, Dec} = {31d, +14d}.)
From vector analysis we have r_hat . E_hat = || r_hat || || E_hat ||
cos[G] = cos[G], where G is the angle between the two unit vectors from
the RA-Dec and alt-azimuth frame fields. We want to find out what the
rate of change of this angle G is when our mount tracks in RA, so we
now differentiate
both sides with respect to R. (d/dR) (r_hat . E_hat) = -Sin [G] dG/dR.
By
using the relation sin^2 + cos^2 = 1 again, we therefore get an
expression
for dG/dR. But we already have the expressions for r_hat and E_hat, so
all
I needed to do was to plug them into Mathematica. Furthermore, what we
really want is dG/dt, the rate of rotation with time, so we do dG/dt =
dG/dR x
dR/dt, where dR/dt is simply the rate of rotation of the earth, which
is
2 pi (i.e. 360 degrees) divided by one sidereal day (23.93446965
x
60 x 60 seconds).
dG/dt =

where the units is in radians
per second, R is our pseudo-RA coordinate, D is our pseudo-Dec
coordinate, and L is our observer's latitude. To convert D to the usual
declination d, note that for D = 0 degrees, d = +90 degrees; D = +90
degrees, d = 0; D = +180 degrees, d = -90 degrees.)
One of the practical applications of the above formula is the
following. I have been thinking of discarding my heavy equatorial mount
and small telescope and replacing it with a large Dob with a driven
alt-azimuth mount. However, I want to use it to do high resolution
photography of the planets. The question is how long an
exposure can I make without having my image
smeared and blurred by field rotation?
To consider this let's suppose the radius of our planet is sigma in arc
seconds. We shall also assume that our planet is placed right at the
center of our field of view; one should keep this in mind when doing
planetary photography. After a time tau seconds, the planet as seen in
my Dob would have rotated by roughly dG/dt x tau radians; which means a
given point on the circumference would
have moved by an angular distance of dG/dt x tau x sigma. (The exact
expression can be obtained in at least two ways. One would require
replacing R with an appropriate time dependent expression - e.g. R = 23.93446965
x
60 x 60 t - in the above formula, and then integrating it with respect
to t over the appropriate limits. The other would be to replace R, with
the time
dependent expression, in
the just-worked-out r_hat . E_hat = Cos[G] and then plug in the appropriate starting and
ending times to obtain two
separate sets of equations, take the inverse cosines
of both sides, and subtract.) Because the
circumference of the planet would be most smeared, it suffices to
ensure that a given
point on the circumference would not appear smeared after a given time
tau.
Now to have a smeared image the angular distance traveled by a given
point
must be greater than roughly half the smallest angular distance that
can
be resolved by the telescope. The latter (in radians) is given by a
well
known formula: 1.22 x lambda / diameter of scope, where lambda is the
wavelength
of light - since we are looking for the maximum allowed time, we may as
well plug in the shortest wavelength (i.e. the most sensitive) of
visible
light: 4 x 10^-7 m.
This means dG/dt x tau x sigma < (1/2) (1.22 x 4 x 10^-7) /
Diameter, which leads to the maximum allowed time tau is

where R, D and L are as before, Gamma is the diameter of the telescope
in inches, and Sigma is the radius of the planet in arc seconds.
As a concrete example, for the August 2003 opposition of Mars, the red
planet would have a radius (sigma) of roughly 12'' and declination of
approximately
+14 degrees (D = 90 degrees - 14 degrees). If I'm observing from
Singapore (latitude of 1 degree, which
I will round off to zero) with a 10 inch Dob, the following is the plot
of
maximum allowed exposure time over the entire movement across the sky
(i.e.
over the range of R from 0 to 2 x pi).

As you can see the minimum is greater than 135 seconds, or 1 min 15 s.
This is very sufficient for planetary photography since exposures
rarely exceed several seconds (not advisable anyway, due to
turbulence).
Even if the planet is placed off center by a distance of say 10 radii,
we
would still have a minimum of 13 seconds, adequate time for photography
with
webcams and high speed films. However, this illustrates why alt-azimuth
mounts
without field rotators are impractical for deepsky astrophotography
since
the relevant radius (sigma) in that case much greater, and hence the
maximum
allowed time is much shorter, while the exposure time needed is usually
at
least tens of minutes.
Part II: Equatorial Mounts
A little thought reveals that we can use our results above to solve a
related problem in deepsky astrophotography for equatorial mount users.
It is impossible to achieve perfect polar alignment. This error in
polar alignment leads to field rotation problems similar to the one
described above. The natural question is then, how close to the true
pole must one align his/her equatorial mount axis in order not to
suffer from field rotation effects in a guided photograph for a given
desired length of exposure?
Earlier, we used the {e, a} coordinate system to represent movement by
the alt-azimuth mount - images viewed through a scope placed on such a
driven mount would not rotate with respect to the local {e, a} grid.
Now we can use the same {e, a} grid to represent movement by an
equatorial mount, except the grid would now have to be rotated such
that the e = 0 point (i.e. the mount's north pole) would be located
close to the D = 0 point (i.e. the north celestial pole), where the
angular distance between the e = 0 point and D = 0 point as measured
from the center of the sphere (0, 0, 0) would then be the error in
polar alignment. But this is simply equivalent to the above problem if
we observe that the variable w = (90 - L) degrees we used above is
exactly the polar alignment error we are currently pursuing.
By replacing L with (90 - w) degrees, I went on to find out, for a
given exposure time, which areas of the sky would not suffer from field
rotation effects when photographed. By assuming that I use a perfect
autoguider guiding on a star right at the center of my photograph, I
made plots for my 5" refractor (770mm focal length), which gives
approximately a 2.68 degrees wide field on the 36mm side of the 35mm
film format.
First I looked at the case for a 20 minutes exposure.
Polar alignment Error: 1.5 degrees (Vertical Axis:
D, Horizontal Axis: R)

Polar alignment Error: 1 degree (Vertical Axis: D,
Horizontal Axis: R)

Polar alignment Error: 0.5 degree (Vertical Axis:
D, Horizontal Axis: R)

Polar alignment Error: 0.15 degree (Vertical Axis:
D, Horizontal Axis: R)

These plots show the regions of sky
that can be photographed with my 5" refractor without suffering from
field rotation effects over a duration of 20 minutes. The vertical axis
is our pseudo-Dec coordinate (in radians), which means the top of the
plot is the celestial north pole, the middle are the mid-latitudes, and
the bottom is the south pole. The horizontal axis is our pseudo-RA
coordinate (in radians), which means if you look at the plot from left
to right you are looking at the sky from the eastern hemisphere
meridian
to the western hemisphere meridian and then back to the eastern
hemisphere meridian (actually east and west is dependent on your
definition, but I hope one gets the idea - if not look at my first
diagram on this page). The white areas are the regions in the sky that
can be photographed without suffering from field rotation effects,
whereas the colored regions cannot. (These diagrams are really 3D plots
of (x, y, z) = (R, D, tau). We are viewing them 'face-on,' from the
'bottom,' in order to achieve this seemingly 2D perspective, ignoring
the tau axis.)
We observe immediately two things. The first is that the polar regions
suffer the most from field rotation effects; or to put it in another
way, if you wish to photograph the polar regions, you'd need to polar
align your mount much more accurately than you'd need to for
photographing the equatorial regions. The second is that polar
alignment for deepsky astrophotography really needs to be accurate - we
see that even with an error of only 1 degree and a relatively short
exposure of 20 minutes, roughly 35 degrees of sky around each pole
cannot be photographed successfully.
Here are two more examples for the same telescope. The first is for a 1
hour exposure.
Polar alignment Error: 0.5 degrees (Vertical Axis:
D, Horizontal Axis: R)

Polar alignment Error: 0.15 degrees (Vertical
Axis: D, Horizontal Axis: R)

Polar alignment Error: 0.05 degrees (Vertical
Axis: D, Horizontal Axis: R)

The second example is for a 2 hour exposure. Notice how accurate polar
alignment needs to be for this case - even a 0.5 degree error in polar
alignment leaves much of the sky unsuitable for photography.
Polar alignment Error: 0.5 degrees (Vertical Axis:
D, Horizontal Axis: R)

Polar alignment Error: 0.15 degrees (Vertical
Axis: D, Horizontal Axis: R)

We can summarize the results as follows:
1) The larger the aperture of your photographic instrument (the larger
the Gamma), the higher its resolution, and hence the more sensitive
your photograph will be to mis-polar alignment.
2) The wider the field of view of your photographic instrument - and
hence the larger the radius of rotation (sigma) - the more susceptible
your photograph is to mis-polar alignment errors.
3) To minimize field rotation problems, always try to guide near the
center of your photograph. The key is one needs to minimize the angular
distance between the guide star and the farthest point from it in your
photograph.
4) Be especially careful in polar alignment when photographing near the
poles.
Part III: Declination Drift
We can
solve yet another problem quite easily, with the work already done
above. This is the issue of declination drift. When performing polar
alignment, astrophotographers usually use what is called the drift
alignment method for polar alignment. After roughly aligning the polar
axis of her/his mount to the north, the astrophotographer usually
proceeds to point her/his telescope to a star low in the east (or
west), center it on usually a crosshair and watch which way it drifts
in declination as the mount tracks the star with its motor drive on.
There is a standard procedure to determine the corresponding
adjustments needed. (With a little extra effort, one can also derive
the procedures from the current discussion.) Next the astronomer looks
at a star on the meridian and performs similar observations and
adjustments. The question that then naturally arises is, how much
declination drift within a given time interval is acceptable if one
desires to obtain a non-field rotated photograph - i.e. the field
rotation effects do not smear the stars sufficiently to be noticeable?
First I recall a result I obtained above, but did not display. I
calculated the cosine of the angle G (Cos[G]), which in the present
case is really the angle between the instantaneous direction of
movement of the telescope's center of view and that of the star at the
center of its view at a given moment. Now the earth and the mount
rotate at a rate of u = (2 Pi) / (23.93446965
x
60 x 60) per second. That means in a small time interval, the apparent
movements of the center of the telescope's view and the star would
appear to each trace out a line, which when taken together forms a
small wedge. This small wedge can be taken as a flat triangle (in
Euclidean space) as a first approximation - even though they actually
sweep out arcs on the unit sphere defined above. Then, assuming the
angle of the wedge is small, we can further assume that the declination
drift can also be approximated by the circular arc subtended by the two
lines forming the wedge, even though to be precise we'd need to resolve
it into perpendicular (aka declination drift) and parallel (aka RA
drift) components and also take into account the curvature of our unit
sphere.
Let t be the time that has passed since our astronomer began watching
the star. Both the telescope's center of view and the star would have
swept out an angular distance of (u t). That means the distance between
the ends of the two lines is, roughly G x (u t). That is our desired
declination drift, in radians:
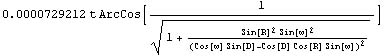
For the same formula in arc seconds - a more useful unit for practical
declination drift purposes, we divide by 2 Pi and multiply by (360 x 60
x 60) arc seconds:
 [Dt]
[Dt]
where t is the total amount of time in seconds star has been allowed to
drift from the center of view, w is the angular distance the true
celestial pole is displaced from the mount's polar axis (aka polar
misalignment), D and R are the pseudo-RA and Dec coordinates defined
above in Part I.
Suppose we have figured out - say from the considerations described in
Part II above - that we need to get the mount's polar axis within w
radians (or degrees - whichever you wish to plug in) of the true pole.
And suppose we're only patient enough to watch the star drift for t
seconds (e.g. a common time used is 300 seconds, or 5 minutes). Then
how much can the star drift within this t time without giving smeared
pictures?
The answer depends on what direction the mount's pole is displaced from
the true pole. Let's first note that the arc on the unit sphere R = 0 /
R = Pi is also the direction in which the poles are displaced from each
other on the coordinate system defined. The horizon can of course be
oriented in any way with respect to the coordinate system I defined
above. That is why we need to perform drift alignment on stars at the
meridian and low in the east or west. To see this, let's observe that
if our mount's polar axis is displaced along the true meridian, then on
the true meridian our mount's constant declination lines (lines that
our telescope's center of view will sweep out on the celestial sphere
when the mount tracks an object) will be parallel to the true constant
declination lines on the celestial sphere, and the two sets of
declination lines will intersect at the largest angle 90 degrees away
from the meridian. That means in such a case there will be no
declination drift if we do drift alignment on a star on the meridian
and the most severe declination drift can be observed 90 degrees away
from the meridian; this also can be seen by putting R = 0 or R = Pi in
the above formula, since ArcCos vanishes when its argument is unity. On
the other hand, if the mount's pole is displaced 'east' or 'west' of
the true pole, then the mount declination lines and the true
declination lines will be parallel roughly (I say roughly, because
'east' and 'west' is not orthogonal to the direction of the meridian,
and so this is an approximation for small displacements) 90 degrees at
the meridian and intersect at the largest angle on the meridian. (When
I have more time, I'd draw a picture to illustrate this; perhaps some
kind reader can contribute to this?)
To summarize, here is how we do drift alignment. After we do our rough
alignment, we look at stars 90 degrees away from the meridian (so the
above statement regarding low in the east or west is not entirely
accurate) to watch for drift. This is to check for magnitude of the
component along the meridian of the displacement of the mount's pole
from the true pole. Then we watch for drift on a star on the meridian.
This checks how far the mount's pole is from the true pole in the
'east' or 'west' direction. (Remember these statements are
approximations, good for small displacements - this is reasonable since
we have already assumed that rough polar alignment has already been
done.) We repeat this procedure until the corresponding adjustments we
make reduce the drift to a level that is low enough, say alpha arc
seconds in t time, for both stars on the meridian and 90 degrees away
from it.
Where does our formula come in? As discussed above, w, D and t are
known quantities - in fact quantities determined by the
astrophotographer. (D is the pseudo-declination of the star that one
is doing drift alignment on - to convert to the usual declination,
please look at Part I.) We know the maximum declination drift is
produced when R = 0 in our above formula. Therefore a necessary (but
alas not sufficient) condition that we have met our required standards
for drift alignment is when the total amount of drift (alpha) observed
in the telescope is less than the answer one obtains when plugging our
values for w, D, R = 0, and t into the above formula [Dt].
July
2005: Putting R = 0
(see below) completely removes dependance on w and D, since sin[0] = 0.
Because of
this I suspect the necessary condition imposed by [Dt] is too weak to
be truly useful.
(Footnote: In order to derive the sufficient condition for the accuracy
needed, one would have to do further analysis. Specifically, here is
one possibility: w would have to be resolved into the displacement
along the meridian and also along the 'east' or 'west' directions (say
p and q respectively). Given a particular mount setup, obtaining two
measurements on the declination drift of stars on the meridian and 90
degrees away from the meridian would give us, after plugging them into
[Dt] a pair of simultaneous equations that could be solved - by
software! - for the values of p and q. Then, provided you could make
accurate adjustments on the altitude and azimuth axes of the mount (an
unfortunately non-existent feature, as far as I know), it would be
possible to obtain very quick polar alignment - no need to perform
tedious repetitions of the drift alignment procedure - to a degree of
accuracy limited only by the accuracy of the mount's altitude and
azimuth adjustment system and of course the accuracy of the drift
measurements.)
Yi-Zen
August 2003
(Last Updated Jan 2004)
References
Eric Weisstein's World
of Astronomy (Sidereal Day page): http://scienceworld.wolfram.com/astronomy/SiderealDay.html















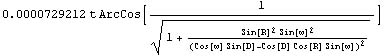
 [Dt]
[Dt]